Animated Demo	Static Demo

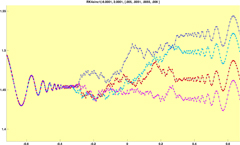
Plot of the function df(x)/dx = sin(1/x^4) showing numerical breakdown for varying step sizes of the approximation, which uses 4th order Runge-Kutte equations.

Step sizes are chosen to avoid the mathematical singularity at x = 0.0 . As the ratio of the differential equation feature size to the solution step size shrinks ( note that frequency approaches infinity as x approaches 0.0 and hence the feature size also approches zero ), the fixed step sizes ( step = { 0.005, 0.0051, 0.0055, 0.006 } ) become too large to validly approximate the solution to the differential equation, causing stepwise approximations to diverge from the "true" solution. After passing the singularity at 0.0 each of the step sizes reacquires the shape of the true solution, but with differing y offsets, depending on where (vertically) the errant approximation is when the feature size of the differential equation solution becomes large enough that the stepwise approximations once again represent a valid approximation to the system.